個のグループ（
）が存在しているとする。そして、どのグループに所属するか既に分かっている観測対象データを保有しているとする。しかし、どちらに所属するか判然としないデータを収集した時、既に所属の分かっているデータに基づいて、所属不明のデータがどちらに所属するかを予測する。これが判別分析である。
判別分析について
まず、分析に用いる「判別分析（Discriminant Analysis）」について説明する。判別分析とは、観測する対象データが、どのグループに所属するかを予測する手法である。たとえば、良い・悪いの２グループや合格・不合格の２グループ等である。この予測の事を「判別」と呼ぶ。２つ以上の分類も可能であり、分類が２つの場合を「２群の判別」、３つ以上の場合を「多群の判別」と言う。
具体的には、まず個のグループ（）が存在しているとする。そして、どのグループに所属するか既に分かっている観測対象データを保有しているとする。しかし、どちらに所属するか判然としないデータを収集した時、既に所属の分かっているデータに基づいて、所属不明のデータがどちらに所属するかを予測する。これが判別分析である。
２群の場合を説明する。データが、２群に分かれる事が分かっており、そのデータを観察する指標（企業の財務指標など）を
とする。その時、データの散布図を描いてみると、以下の様になる（図１）。この時、座標軸
を考えると、各データがこの座標軸上でとる値は、
となり、一つの合成変数（総合的指標）の形になる。また、各
だけでは（各軸上の分布図を参照）データ同士の重なり合いが大きいため、２群の判別の決定的要因に欠けるが、
両方を用いれば（座標軸
上の分布図を参照）、データがきれいに分かれて２群の判別が可能である。
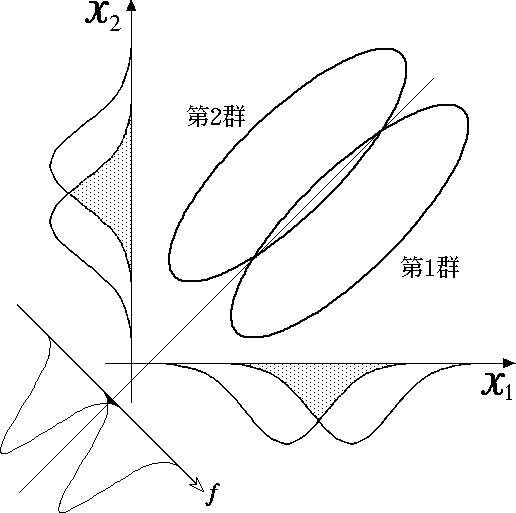
（資料）群馬大学社会情報学部（2000年2月）。
今回の分析では、銀行の「倒産」「非倒産」の２分類を行う。２群の判別分析を行う方法には、主要な方法として５つある。それらは、①マハラノビスの距離による方法、②線形判別関数による方法、③正準判別分析による方法、④重回帰分析による方法、⑤ロジスティック回帰による方法である。回帰分析は基本的に、説明変数（
）を用いて目的変数（
）の「量の予測」を行うものである。それに対して、これら５つの方法は全て「質の予測」を行おうとするものである。因みに、２群の判別分析においては①～④の方法全て、理論上同じ結果を導く。今回の分析では②の方法を用いて行う。以下では、この②の方法について具体的に説明する。なお、①は②の手法と大きく関わるので、合わせて具体的手法を述べる。
個の群の母集団平均（重心）を
、観測値を
とする。そして、各群の分散共分散行列を
、その逆行列を
とする時、下記の（１）式による各群までのマハラノビス距離という値を計算する。そして、各群の各データは、各群へのマハラノビス距離値が最も近い群に属すると判定する。
（１）下の図２を見てもらいたい。楕円で描かれた各群の中央の点が、母集団平均（重心）である。そこからある点へ向かって伸びている線がある。この線がマ
ハラノビス距離を示している。しかし、実際のこの線距離とマハラノビス距離は異なる事に注意したい。簡単に言えば、マハラノビス距離は長軸方向と短軸方向では異なり、短軸方向（楕円の幅の狭い方）の距離が長い。
あるデータから第１群の重心へのマハラノビス距離を
、第２群の重心へのマハラノビス距離を
と表す時、
ならば第１群、
ならば第２群に属すると判断する。
と
の関係を用いたものである。
ならば第１群、
ならば第２群であると、先に述べたが、それぞれ移項すれば
の時は第１群、
の時は第２群に属すると言い換えられる。
この時、
とおけば、
の値が正か負かで判別する事が可能である。この式を判別関数と言う。詳しくは以下の通りである。また、前提条件として各群の各変数が多変量正規分布をとり、各群同士の分散・共分散行列が共に等しい事（等分散性）が、分析に当たってまず求められる。
もしも、各群の分散・共分散行列が等しい、即ち
が仮定できれば、先の（１）式は次の（２）式の様になる。
（２）
第１項は各群に共通、第３項は各群ごとに異なる定数（これを
とする）である。各ケースごとに異なるのは第２項のみであるため、次の（３）式の計算を行えばよい。
（３）
係数
は、
の要素を
とすれば（４）式によって求めることができる。
（４）
（４）式の第１項は群に関係ないため無視する事ができる。よって、下記（５）式の数値が最も小さい群に属すると判定すればよい。（５）式は、分類関数と呼ばれる。
（５）
また，マハラノビス距離の大小を比較する代わりにあらゆる２群の組合わせに対して、（６）式で表される
個の判別関数を定義しておくこともできる。第１群と第２群の判別関数は、
（６）
となる。
また、本稿では触れないが各群間の分散・共分散が共に等しくない場合、１次の線形関数は適用できない。等分散性の検定を行い、その結果不等分散である時は２次の曲線判別関数を適用する。これにより、共分散を考慮して重心に近い群へ判別する事が可能となる。更に、各変数が多変量正規分布をとる事も条件であり、非正規である場合はノンパラメトリック法を適用する。